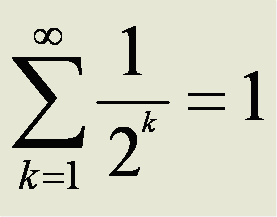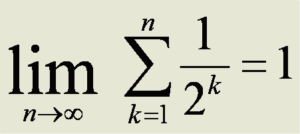In 1998 when the accelerating expansion of the universe was reported by two groups, the astrophysics community shortly declared the existence of some kind of “dark energy”. While no one knew what this was, physicists invoked things like Einstein’s Cosmological Constant and vacuum energy to fit it to various theories. As John von Neumann famously quipped, “With four degrees of freedom I can fit an elephant.” While there are theories that attribute the acceleration data to local rather than global effects or sampling issues let’s assume the acceleration is real and global. If so and the acceleration is caused by dark energy / vacuum energy / cosmological constant, the universe may come to a practical end in terms of habitability in 500 billion years or so. This is a long time and may be an optimistic estimate.
Here’s an alternative to dark energy. The starting point is the question: Why are we here — now? The philosophical name for this is the doomsday argument. The basic idea is that while the universe is supposed to last for trillions of years fading into a heat death, here we are at the very start, only 13.8 billion years in, only 1% of the first trillion years. Since the early universe did not generated the elements needed for life, the ratio is even worse. Being born “now” in the universe seems unlikely. Locally, even with speed of light limitations, we should be able to spread around our galaxy in no more than a few million years. We have found out recently that most stars have planets. Out of the 400 billion star systems in the Milky Way, there are perhaps a billion suitable planets that we could populate. If that is going to happen, finding ourselves on a single planet out of a possible billion is unlikely. If you reach into a jar with 10 balls numbered 1 through 10 and pull out number 6, nothing seems odd. If you reach into a bin with a billion balls, numbered 1 through 1,000,000,000 and pull out number 6, that’s weird. This is a known problem in statistics with a well defined confidence interval based on how close you are to the start of something. What it boils down to is that a random sample can be expected to occur between 3 and 97 percent of the range. If you pull out a 6 the first time you can be 95% confident that there are between 7 and 200 balls total. After 13.8 billion years we can expect the universe to last from 200 million to 445 billion years from now. Homo sapiens have been around for 200,000 years, so to be here now, we expect H. sapiens to last another 6 thousand to 6 million years. The implication is that we may not be around long enough to populate the galaxy and/or the galaxy may not be around as long as we think it will be. The first possibility involves things like global nuclear/biological war, asteroid strikes, and the like. The second possibility is the subject of this post.
We are alive at about the earliest time possible in the history of the universe. Modern scientific discoveries have moved this forward. The original Milky Way consisted of population 3 stars made up of hydrogen and helium and little else. Life was not possible. Some of these stars ended their lives as supernovae creating and ejecting elements like nitrogen, oxygen, calcium, phosphorus, and carbon necessary for life as well as iron and nickel useful for making solid planets. These enriched the hydrogen clouds that eventually were swept into the formation of population 2 stars, some of which ended as supernovae producing the additional elements that went into the formation of population 1 stars like our sun 4.5 billion years ago which is already 2/3 of the current age of the universe. So far, so good. Fifty years ago the assumption was that the solar system was typical and life was inevitable. The earliest life appeared nearly 4 billion years ago. It took 3.5 billion more years for anything more advanced than bacteria to appear. 450 million years later we’re here. Presumably other paths would create self-aware life earlier.
Then modern science complicated the picture. While we have discovered that most stars have planets, the solar system is atypical and most systems have hot Jupiters and other barriers to the kinds of planets that are needed for life. In our system, the Jovians, rather than eating the terrestrial planets, protect them by clearing the inner system of asteroids and comets. Quite unusual and unlikely.
Then there’s the Moon. The Moon is by far the largest moon compared to the planet it orbits. It is responsible for tides that may have been necessary to enable the movement of life from the seas to the land. More importantly it stabilizes the earth’s rotation axis, keeping the seasons regular. Without it, the earth would slowly tumble, alternating freezing and desert climates, and preventing the emergence of complex life forms. But the moon is almost impossible dynamically. As a result of the Apollo sampling missions and modern computer simulations we have a pretty good idea what happened. At some point a few tens of millions of years after the formation of the solar system a fortuitous Mars sized body slammed into the earth at just the right angle and speed to create a spinning disk of rubble that eventually settled into the earth and the orbiting Moon … an extraordinarily unlikely event.
Uranium is the next issue. The radioactive uranium in the earth’s interior has kept the iron/nickel core molten for the last 4.5 billion years. This allows the core and mantle to produce a magnetic field. This field shields the the earth and the life on it from the solar wind and solar flares. Without it the earth would be a radiation seared wasteland like Mars and the Moon. The problem is, where did the uranium come from? We know it was not part of the early universe. And it turns out, the supernovae that produce lighter elements are not able to produce uranium. No uranium, no life. Enter LIGO, the gravity wave observatory. Analysis of the gravity waves yields a possibility. Most of the “visible” events are black hole mergers that yield no material output other than gravity waves. Similarly black hole / neutron star mergers only produce gravity waves. A few of these events are mergers of orbiting neutron stars. These produce an outpouring of large nucleus elements including uranium in addition to gravity waves. While in the minority, we finally have a source for uranium, sort of. To have a merger of neutron stars we have to start with two orbiting stars both between 10 and 29 times the size of the sun, no more, no less. Smaller stars turn into white dwarfs without the density to create uranium in a collision and larger stars turn into black holes that do not release anything. These two stars have to live out their lives, both supernovae without disrupting the other producing orbiting neutron stars. These then slowly spiral in and merge and explode. This takes a long time and is quite rare. This has to happen near a population 1 star forming region to seed the gas clouds with enough uranium for life friendly planets. This would be relatively nearby and 5-6 billion years ago for us. LIGO sees these events from all over the universe every few weeks, but since there are about a trillion galaxies in the universe, there may only have been one in the our entire Milky Way galaxy prior to the formation of the solar system. This tightens the constraints even more and indicates that we are really living at the earliest time possible , which makes a long future for the universe even more unlikely.
Consensus in the astrophysics community is that our universe is a finite unbounded space, probably a 3-sphere embedded in 4 space, just like our planet is a 2-sphere embedded in 3 space. A recent astronomical geometrical finding indicated that we are indeed in a 3-sphere. As you can travel on the earth’s surface in 2 dimensions forever without reaching an edge, you can travel in space in 3 dimensions forever without reaching an edge. Our 3-sphere universe is probably embedded in a 4-sphere and so on. This hierarchy sounds like an infinite universe but not really. As it turns out the volume for an N-sphere of a given radius only increases up to the 5-Sphere and then starts decreasing rapidly and the infinite sum converges. If you add up the volumes of all the hyper-spheres of unit radius (say one universe radius) the total volume is 45.99932…, ie. the total of volume all the finite universes is finite. (Yes, it’s turtles all the way down but they get very tiny quickly.) I’m ignoring the various infinite multiverse theories as these appear to be string theorists grasping at straws. A 1-sphere on a 2- sphere is a circle like a fairy ring of mushrooms on the surface of the Earth. The ring has a finite interior that takes up a finite fraction of the surface of the earth’s 2-sphere surface. The ring has a center which is part of the 2-sphere but not on the ring. Earth’s surface 2-sphere has a finite volume that takes up a finite fraction of the 3-sphere we live in. It has a center that is in the 3-sphere but not on the surface. Similarly, our 3-sphere 3 dimensional universe has a finite volume that tales up a finite fraction of the 4-sphere it’s embedded in. It has a center in the 4-sphere that is not in the 3 dimensional 3-sphere universe. That center probably shares 4 dimensional coordinates with the center of mass of our universe and the historic location of the big bang in four space. Our expanding 3 sphere universe spreads through the 4-sphere just like a fairy ring spreads over the surface of the earth. The main point here is that if the total multidimensional universe is eternal and “big bangs” happen on a regular basis, the finite 4-sphere will have already filled up with expanding 3-sphere universes which, if they persist, will be banging into each other.
As scientists were searching (successfully) for the hypothesized Higgs Boson, vacuum decay entered the discussion. This represents the possibility of a point quantum event that disassembles and destroys everything the the universe, with the wave front traveling at the speed of light. While this is considered unlikely, the science is not settled. There is also the possibility that a collision of 3-spheres could trigger such an event. We may live in a soap bubble waiting to be popped. Since most of the universe is beyond our light speed horizon it is possible for such an event to occur without ever reaching us through three space. It is conceivable that shock waves propagating through 4 space are faster than the 3 space speed of light, much like seismic P waves propagating through the earth faster than the surface S waves. While the decay event propagates through the 3-sphere, the shock wave could couple to 4 space and travel across the 3-sphere interior much faster.
Perhaps 5 billion years ago a decay event occurred somewhere in our universe. The initial decay volume produced a pressure shock that propagated in 4 space across the 3-sphere internal volume and inflated the universe slightly. As the surface of the volume of destruction increased, the generated shock increased which increased the inflation of the rest of the 3-sphere. Thus the existing expansion of the universe appears to accelerate. If this event occurred within our horizon, that may explain why we aren’t here much later.
On a happier note, assume the bubble doesn’t ever pop. Two popular scenarios in that case are the Big Rip and Heat Death of the Universe. Both involve runaway expansion leading to an effectively empty, infinite universe. Really boring. Consider the fairy ring — when it’s a few feet in diameter we can imagine it expanding forever — but we know that if it did, it would crunch back together on the other side of the earth (ignoring oceans and deserts). Similarly any Big Rip or Heat Death will eventually meet itself on the other side of the 4-sphere. Who knows, it may start another big bang.
Please leave any comments using the post in my comments category.