This question has been debated by philosophers and mathematicians for at least 2500 years. Plato maintained that there was an actual plane of existence where “ideal” originals of mathematical objects like circles and squares existed. Our imperfect renderings of them were shadows of these ideals. Up until the middle of the nineteenth century, mathematics was the main guide to understanding of our physical world and seemed to be part of it from the mechanics of Archimedes to Kepler’s laws of planetary motion, Newton’s laws of gravity and mechanics to Maxwell’s equations describing electromagnetism. It seemed obvious that the laws of the universe were mathematical.
Starting in the mid 1800’s Riemann’s non-Euclidean geometry, Cantor’s hierarchy of infinities, and work on the foundations of mathematics were making mathematics more and more abstract and divorced from any connection to the physical world. By 1920 most mathematicians and many physicists doubted that there was any real connection. The physicist Richard Feynman famously remarked that if all of mathematics disappeared it would set physics back about a week.
Around this time Einstein’s general relativity was gaining currency and it became obvious that non-Euclidean geometry was actually part of reality. Shorty thereafter the discovery of quantum mechanics demonstrated that the only possible description of the physics of the microscopic world was inherently mathematical.
In 1960 the physicist Eugene Wigner published an article entitled The Unreasonable Effectiveness of Mathematics in the Natural Sciences discussing the surprising (at the time) fact that some mathematics corresponded so well to the physical world that it could be a guide to discovering new physics and even making empirical predictions. In a similar vein Richard Hamming wrote: My first real experience in the use of mathematics to predict things in the real world was in connection with the design of atomic bombs during the Second World War. How was it that the numbers we so patiently computed on the primitive relay computers agreed so well with what happened on the first test shot at Almagordo? There were, and could be, no small-scale experiments to check the computations directly. Later experience with guided missiles showed me that this was not an isolated phenomenon – constantly what we predict from the manipulation of mathematical symbols is realized in the real world.
It seems clear that the truth is somewhere in the middle. Reality has objects – be they atoms, asteroids, or galaxies that can be numbered and compared using integers and rationals numbers. Geometry corresponds too well to the space and extent of reality to be coincidental. The non-Euclidean geometries have their place in the Minkowsky space of Special Relativity, the curved space of General Relativity, and in double elliptical form, surveying of the earth. Group theory captures the symmetries and conservation laws of nature. Even number theory, celebrated by the mathematician G.H. Hardy as having no practical applications, now is crucial to cryptography, electronic commerce, and even positioning radio telescope dishes. Analysis and calculus capture the dynamics of the universe. Any space alien on the other side of the galaxy at least as advanced as Archimedes will know about π and the Fundamental Theorem of Arithmetic. All this is in the universe to be discovered.
Much of modern and some older mathematics however is purely an invention of the human mind. Mathematicians have spent a fair amount of time working through the contradictions, conundrums, and paradoxes involved to create a consistent logical framework. Much of this has been absolutely brilliant work performed by some of the greatest mathematicians who have ever lived. Keep in mind here that mathematics is not physics and is, at root, simply that which mathematicians get paid to do. (I only recently learned that there is a polity for this: If your ideology denies the existence of objective truth, you are forced to maintain that all mathematics is invented.) Here’s a list of inventions:
(1) Infinity is not part of the universe. It is purely the result of human imagination. In a 1926 paper entitled On the Infinite, David Hilbert wrote “the infinite is nowhere to be found in reality” but he noted that the concept is very useful for some parts of mathematics. Consensus in the astrophysics community is that our universe is a finite unbounded space, probably a 3-sphere embedded in 4 space, just like our planet is a 2-sphere embedded in 3 space. As you can travel on the earth’s surface in 2 dimensions forever without reaching an edge, you can travel in space in 3 dimensions forever without reaching an edge. Our 3-sphere universe is probably embedded in a 4-sphere and so on. This hierarchy sounds like an infinite universe but not really. As it turns out the volume for an N-sphere of a given radius only increases up to the 5-Sphere and then starts decreasing rapidly and the infinite sum converges. If you add up the volumes of all the hyper-spheres of unit radius (say 1 universe radius) the total volume is 45.99932…, ie. the total of volume all the finite universes is finite. I’m ignoring the various infinite multiverse theories as these appear to be string theorists grasping at straws.
For centuries mathematicians struggled with infinity and the impossibility of doing mathematics with it: What does ∞/∞ mean? If 1/∞ = 0 then 0 x ∞ = 1 but it also equals any other number as well. There was no “natural” way to handle infinity to be discovered. Mathematicians had to create new mathematics to work with the concept. In calculus the problem of infinity was solved by the concept of limits. The following summation equations are now considered to be equivalent but consider the first.
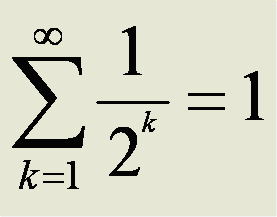
Although this is apparently a standard sum it does not follow the rules for addition. It is not commutative. (You can’t add it from right to left.) By the same token it is not fully associative.
Here’s the “commutative” version of the above which clearly doesn’t work:
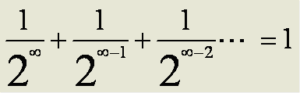
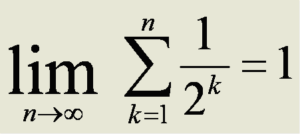
This second summation, while “equivalent” is fully commutative and associative. Modern mathematicians understand that this is what is meant by the first version but it was really confusing 400 – 500 years ago.
The problem is trying to use infinity as something you can reach or a value that can be assigned to a variable. It is not obvious that the mind can truly imagine infinity (as opposed to a really, really big number). Infinity can be used as a direction, or “and so on”, or a limit but trying to use it as an actual number or pretending you can get there, while a part of mathematics, puts you firmly in Wonderland in terms of reality.
(2) Self-reference is not part of the physical universe. Most if not all paradoxes rely on self-reference for their action. Observe a trivial example:
The next sentence is true. The previous sentence is false.
Clearly if the first sentence is true, it is false – a paradox. Much of modern mathematics also relies on self-reference such as Gödel’s Theorem or the modern definition of a set. Russel’s Paradox was created at the dawn of set theory by self-referential sets.
The universe doesn’t appear to contain self-reference or even abstraction unless you want to count the holographic principle which is more like two views of the same object. Going back to the simple example earlier, self-reference, paradoxical or not, involves a flow or motion that circles back on itself. First there is the logical evolution through logical statements to the conclusion that turns back on itself and potentially modifies part of the past. Wherever you have self-reference there is the danger of a circular paradox. The universe apparently eliminates any chance of this by freezing the past and outlawing time travel. In the invented part of mathematics self-reference is just fine – as long as you are really careful. Bertrand Russell and others spent years patching the self-referential holes in set theory.
(3) Axiomatic systems are obviously invented. Our space alien friend is clearly not going to “discover” our axioms. A philosophical problem with sets of axioms is the hubris that leads a person to assume that they can, apriori, capture all the truths and relations of a branch of mathematics in a short set of statements. This is generally not even true. Gödel demonstrated the problem with something as simple as arithmetic. Euclid’s fifth postulate was argued over for 2400 years and eventually subsumed in modern times. Even the most carefully crafted modern set theory axioms cannot capture or define a particular mathematical system, and according to the Löenheim-Skolem Theorem, they can be satisfied by completely contradictory mathematical structures. Axioms are like the rules of a game such as chess or go and can lead to vastly interesting results. Axioms can also be like the rules of golf or baseball and can lead to all kinds of contentions. In any case they are, in a sense, arbitrary.
(4) Sets are totally a product of human imagination. These are relationships among objects, real or imagined, that are absent from the universe. About 130 years ago mathematicians got the idea that an obscure object in combinatorics, the set, could be used to patch up the logical foundations of mathematics which were tottering. It was a classic case of the tail wagging the dog. Trying to stretch sets to encompass all of mathematics resulted in paradoxes and tsuris leading to “solutions” like Russell’s type theory which is strongly reminiscent of the epicycle theories used to patch up the earth centered Ptolemaic solar system models. Axiomatic set theories such as Zermelo-Frankel attempted to bring order to the ensuing chaos with limited success. The ultimate result was a whole spectrum of axiomatic set theories, all different, and all resulting in a different mathematical structure, kind of like with and without a designated hitter, only worse. Adding axioms to Z-F like the axiom of choice or the continuum hypothesis lead to things like Banach-Tarski or non-measurable sets. The last has a certain historical poignancy. Classically a standard method of proof since Pythagoras’ time was proof by contradiction: You assume the inverse of ‘A’ and then if a logical progression leads to a contradiction, ‘A’ must be true. By contrast, in the case of non-measurable sets, a contradiction simply leads to the invention of a new kind of set that can’t be measured.
(5) This is a bit of a pedagogical issue but the problem has existed ever since Euclid’s first axiom defined points. To be perfectly clear, there are no points in nature. There are locations, addresses, coordinates – but there’s nothing there. Treating a point as a real object caused all kinds of problems for thousands of years as mathematicians, working to calculate lengths and areas before calculus, tried to figure out how to add up an infinite number of zero sized points to get a given finite line length since a line was made of “points”.
To sum up: Reality pretty clearly runs on mathematical principles and is almost certainly consistent. Reality and math are part of the same fabric even if we sometimes have a little trouble figuring out those principles. There is also a lot of mathematics that has nothing to do with the universe. Peter Woit, a theoretical physicist, believes that this conflict exists in string theory where very abstract models may be impossible to test in any foreseeable experiment. If this is the case, the “string” must be thought of either as real but untestable, or simply as an illusion or artifact of either mathematics or cognition. Finally, if using Zermelo-Frankel set theory axioms with the “axiom of choice” added, you have infinite point sets that allow you, per Banach-Tarski, to disassemble a sphere into five pieces and reassemble the five pieces into a sphere one half the size of the original, (a provable result under ZFC) you are so far down the rabbit hole that Wonderland disappeared in the mirror long, long ago.
