A decades old science fiction theme (or dream) has been the space elevator. This is a (really strong) cable running from the equator through geosynchronous orbit and then on to a suitable stabilization mass. Vehicles running up and down the cable would provide an efficient, low cost, route to planetary orbit and beyond. The technical challenges are immense requiring materials far beyond current state of the art but perhaps possible.
Building such an elevator on Mars presents two additional problems, Phobos and Deimos, the Martian moons which are directly in the path of an equatorial space elevator, unlike Earth’s moon. The blocks below indicate the extremes of the moons’ orbits. One suggested scheme is to create an elevator that sways back and forth under power to miss each moon as it transits, every 11 hours for Phobos and every 131 hours for Deimos. This is recipe for disaster, constantly dodging near misses and hoping nothing goes wrong or wears out in the maneuvering system. Initially it seems reasonable to locate the ground end off the equator far enough that the cable is above the maximum latitudes of the moons with a large enough counterweight to stabilize the revolution. Unfortunately, while stable, there is no way to actually build it. The traditional equatorial based design is built out from geostationary orbit keeping the up and down masses equal until reaching the ground. This is impossible here. With the elevator plane of revolution over the 45th parallel for instance as there is no stable orbit to build from.
However, it may be possible to build it out from one of the poles.
The main idea is like swinging a weight on a rope around your head and then letting out more rope. As long as you spin the rope fast enough the weight does not fall to the ground. While this is a serious mega-engineering project, just making the cable is probably the hardest part. Start with a large, massive structure at the rotational pole. Think the great pyramid at Giza but much bigger. Vertically through the middle is a hollow shaft topped by an eccentric crank with a bearing that connects to the ground end of the cable. The hollow shaft is driven to spin the cable. A streamlined mass is attached to the end of the cable. At initial launch, the eccentric and short cable assembly are spinning fast enough to keep the mass off the ground. The space elevator is is built out from the center through the hollow of the shaft which would probably of kilometer order dimensions. As mass is added to lengthen the cable and increase the counterweight, angular momentum would slow the rotation but increased centrifugal force due to increasing radius would keep tension on the cable. At first the angular drive from the shaft would need to contend with the atmosphere, hence the streamlining, where the drive has greater leverage. This problem will be reduced once the bulk of the mass is outside the atmosphere. With care it should be possible to balance the slow down with the radius increase to bring the end of the cable to a stationary condition at design altitude. At this time the cable will be moving synchronously with the planet which will eliminate drag and the eccentric will be aligned with the cable and no longer turning. By moving the eccentric ahead or behind by turning the shaft slightly, small adjustments to the elevator’s revolution speed or longitude can be effected as the planet’s rotation pulls or eases on the cable.
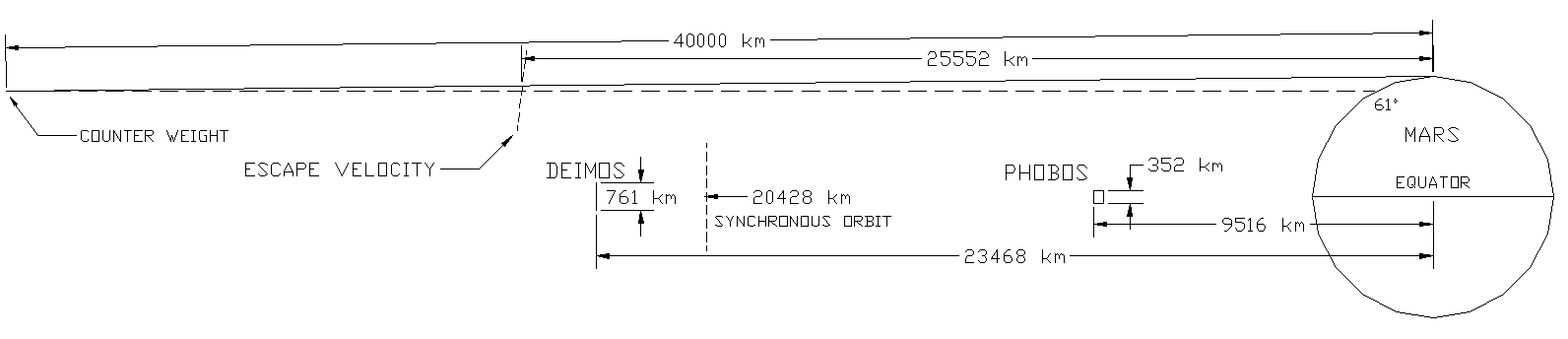
The figure illustrates the geometry for a 40,000km cable. This assumes negligible cable mass compared to the counter weight. Note the escape velocity locus. Any vehicle launched from the cable beyond this altitude will leave the Martian system without other effort. The plane of revolution is the 61st parallel. For this cable length the cable tension at the counter weight is 7.5 times the force of gravity. This makes the system fairly stiff against outside influences. For a 35,000km cable cable tension is 5.6 times gravity and the end is over the 53rd parallel. For a 30,000km cable the cable tension is 3.2 times gravity and the end is over the 43rd parallel. Shorter cables are cheaper but less stable in the presence of outside influences such as gravity from the moons and varying freight and vehicle transportation loadings. The closer the end gets to the equator, the less stable it is.
Please leave any comments in my comments post.
